Rubik’s Cube

These simple routines speed up some of the steps above:

3	if the white face of the corner-piece is on the top face you can use:
	(R U2 R') U'  (R U R')
6	rotate up-layer so only 1 corner is in the correct location then:
	to move 3 corners anti-clockwise - rotate cube so correct corner is front-right then: (starting with your right hand) (U R U' L')  (U R' U' L)
	to move 3 corners clockwise - rotate cube so correct corner is front-left then: (starting with your left hand) (U' L' U R)  (U' L U R')

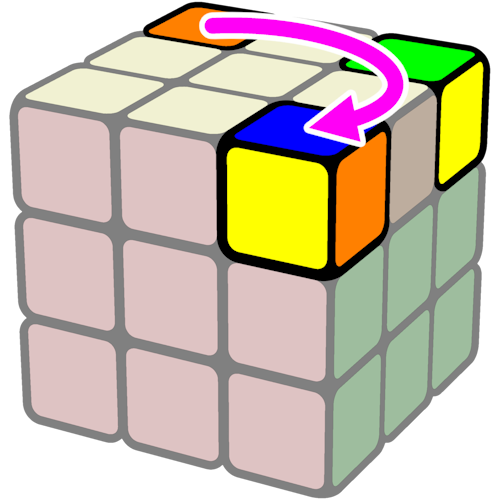Gift wrap: move all the corners of the F, U and R faces clockwise:

 

“Superflip”: flip every edge piece:

show
more

show
less

Note: an easy way to do M' is Rw R'
- reverse it by repeating the algorithm from any orientation!

Also: (...)3  =  repeat (...) 3 times

 

Simply follow steps 3, 6 and 7 for the 3x3x3 cube above.

This is the ‘Reduction Method’ which makes it behave like a 3x3x3 cube - then we can use the 3x3x3 steps above:

1	white 2x2 centre    yellow 2x2 centre (opposite white)    other 2x2 centres (use a white or yellow corner to check which color goes on which side)
2	white edges    non-yellow edges: - position 2 edge pieces so that Lw' or Rw would complete the edge, then:
	Lw' or Rw    U or U'    replace the complete edge with a non-complete edge (using Ln or Rn ) then reverse the previous 2 moves
3	last 2 unsolved edges: - position identical edge pieces so they have the same colour on the F face (as in the diagram) then:
	Uw' (R U R') (F R' F' R) Uw Note: the bit between Uw' & Uw flips the F/R edge 180° To mirror it (i.e. flip the F/L edge): Uw (L' U' L) (F' L F L') Uw'
or
3	last 3 unsolved edges: - position 2 edge pieces as above    move the other, matching top-edge piece as in the diagram, then: (if it’s on the right start with Rw)
	Rw U' R' U Rw'  or  Lw' U L U' Lw Note: these are exactly the same moves as part 2 above
4	final layer - no yellow bar or ‘L’ shape:
	Rw U2 x (Rw U2)2  (Rw' U2 Lw U2 Rw' U2)  Rw U2 Rw' U2 Rw' Note: every right wide (and one left wide) is separated by an U2 This flips the U/F edge 180°
5	final layer - 2 adjacent or opposite yellow edges:
	r2 U2  r2 Uw2  r2 u2 Note: an easy way to do r2 is Rw2 R2'

3x3x3 cube in a cube: move the outside F, U and R faces clockwise:

Note: also works for a 3x3x3 cube

Also: make these all ‘w’ (wide) moves and it will make a 2x2x2 cube in a cube!

 

Stripey sides:

 

 

This is the ‘Reduction Method’ which is very similar (but easier) to the 4x4x4 steps above:

•	for each 3x3 centre: first complete the 3 across the middle, then one edge and then the other
1	white 3x3 centre    yellow 3x3 centre    other 3x3 centres (don’t worry about the order as the centres can’t move - same as a 3x3x3)
	tip: to complete the last 3x3 edge: with 1 corner on the correct face, put the other 2 together on an adjacent face
1a	last 2 adjacent centres each with 1 piece unsolved: (this is an alternative to the tip above) - middle pieces: position unsolved pieces on the left of the F and U faces, then: Lw F' M F Lw' F' M'
	- corner pieces: position unsolved pieces in the top-right of the F and U faces, then: Rw' F' Lw F Rw F' Lw'
2	white edges    non-yellow edges: - same method as 4x4x4
	Note: you can do just 2 or all 3 edge pieces at a time
3	last 2 unsolved edges: - use the same method as 4x4x4 to move edge piece(s) to the opposite side of the F face and flip the edge 180°
4	final edge - correct pieces but not orientation:
	Rw U2 x (Rw U2)2  (3Rw' U2 Lw U2 Rw' U2)  Rw U2 Rw' U2 Rw' Note: same as the 4x4x4 algorithm exept for the ‘3’ This flips the 2 outside U/F pieces (corner and edge on both sides) 180°

“Superflip”: flip every edge piece:

Note: very similar to 3x3x3 Superflip
- reverse it from any orientation - but do the bottom line first!

 

Half “Superflip”: flip the edge pieces of the U, R and B faces:

Note: easily mixed up with the Superflip
- reverse it by doing the bottom line first making sure one mixed-up corner is at the U/R/B corner

 

 

Where pieces need to be rearranged to fit the reduction method.

flip U/F outer edge pieces 180°

4x4x4

Rw U2 x (Rw U2)2  (Rw' U2 Lw U2 Rw' U2)  Rw U2 Rw' U2 Rw'

Note: Rw is the same as 2Rw

 

5x5x5

Rw U2 x (Rw U2)2  (3Rw' U2 Lw U2 Rw' U2)  Rw U2 Rw' U2 Rw'

 

6x6x6

Rw U2 x (Rw U2)2  (4Rw' U2 Lw U2 Rw' U2)  Rw U2 Rw' U2 Rw'

 

7x7x7

and

Rw U2 x (Rw U2)2 (5Rw' U2 Lw U2 Rw' U2)  Rw U2 Rw' U2 Rw'

 

3Rw U2 x (3Rw U2)2 (4Rw' U2 3Lw U2 3Rw' U2)  3Rw U2 3Rw' U2 3Rw'

 

 

flip the whole U/F edge 180°

4x4x4

Rw U2 x (Rw U2)2  (Rw' U2 Lw U2 Rw' U2)  Rw U2 Rw' U2 Rw'

Note: Rw and Lw is half of the cube.

Also: this is the same as the algorithm above as the outside edge pieces of a 4x4x4 is the whole edge (included for completeness and comparison)

 

6x6x6

3Rw U2 x (3Rw U2)2  (3Rw' U2 3Lw U2 3Rw' U2)  3Rw U2 3Rw' U2 3Rw'

Note: actually the same as 4x4x4 in that each nRw or nLw is half the cube.

 

 

swap the F and B edges of the U layer

4x4x4

(r2 U2) (r2 Uw2) (r2 u2)

Note: remember r is the inside right layer (r = Rw2 R2).

 

6x6x6

(3Rw2 F2 U2) (3Rw2 R2 U2 F2) 3Rw2